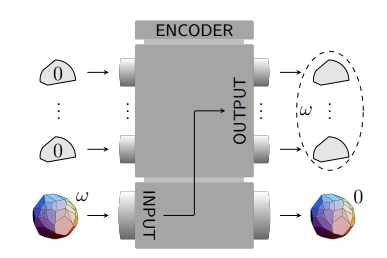
How Quantum Mechanics Derives from a Revolutionary New Theory of Information | by The Physics arXiv Blog | The Physics arXiv Blog | Medium

The Formalisms of Quantum Mechanics: François David | PDF | Hamiltonian Mechanics | Lagrangian Mechanics

Buy Operators and Representation Theory: Canonical Models for Algebras of Operators Arising in Quantum Mechanics (Dover Books on Physics) Book Online at Low Prices in India | Operators and Representation Theory: Canonical
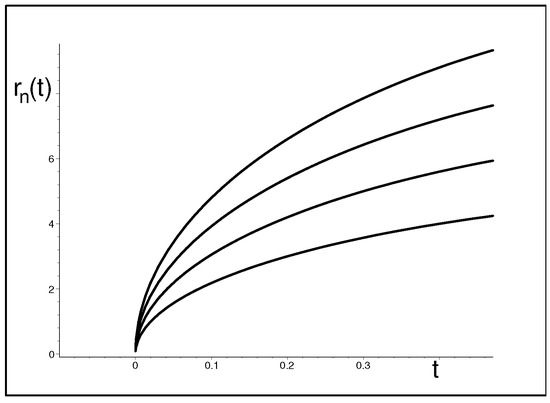
Axioms | Free Full-Text | Quasi-Hermitian Formulation of Quantum Mechanics Using Two Conjugate Schrödinger Equations

quantum mechanics - Can't understand how Griffiths derives an expression in QM text - Physics Stack Exchange

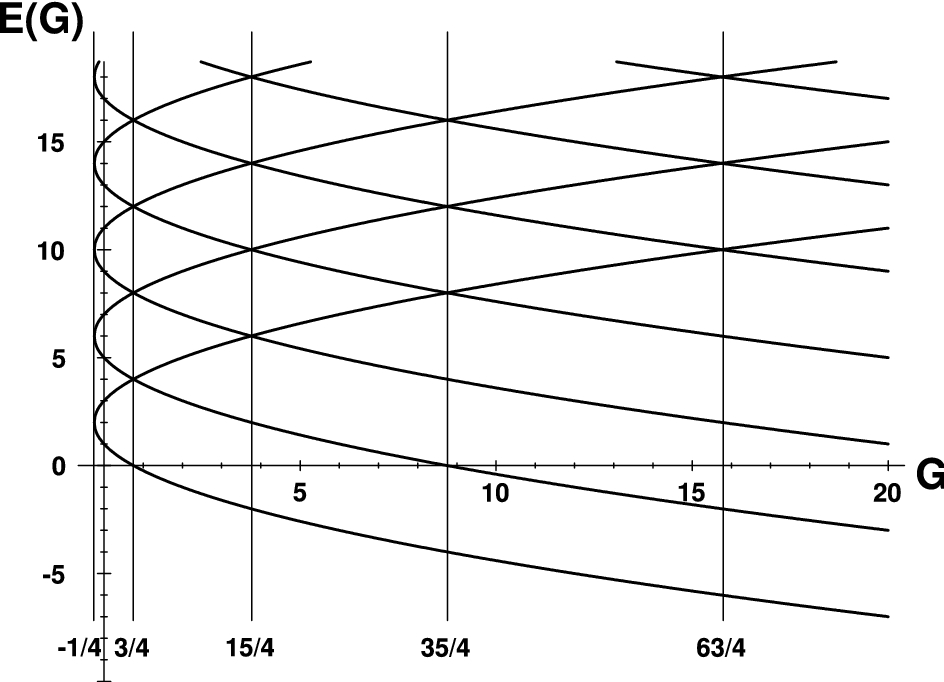






![PDF] Stone´s Theorem and Applications | Semantic Scholar PDF] Stone´s Theorem and Applications | Semantic Scholar](https://d3i71xaburhd42.cloudfront.net/7f61a5298cc3be1c98f24f78d798bf3e963f36f3/57-Figure3.3-1.png)
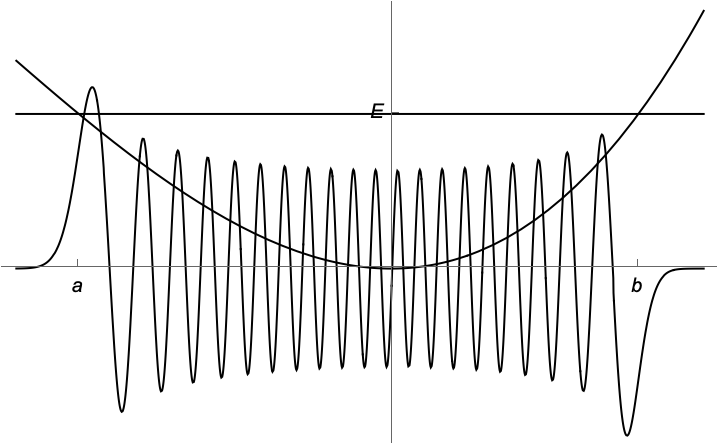


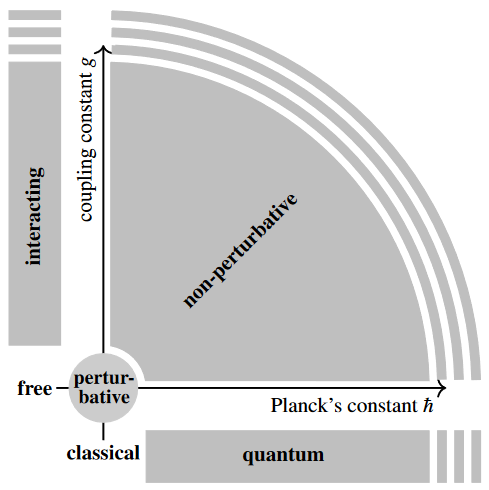


![PDF] Stone´s Theorem and Applications | Semantic Scholar PDF] Stone´s Theorem and Applications | Semantic Scholar](https://d3i71xaburhd42.cloudfront.net/7f61a5298cc3be1c98f24f78d798bf3e963f36f3/56-Figure3.2-1.png)

